Whole-brain t tests and p values

Here we do a whole brain analysis on our example dataset:

import numpy as np
np.set_printoptions(precision=4)  # print arrays to 4 dp
import numpy.linalg as npl
import matplotlib.pyplot as plt
import nibabel as nib
import nipraxis

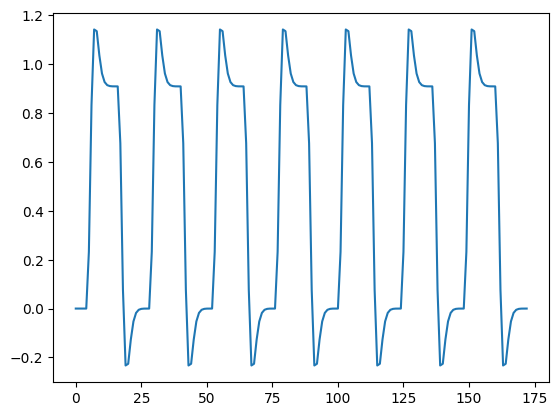
We load the hemodynamic regressor from Convolving with the hemodyamic response function. We used this regressor in Modeling a single voxel.

conv_reg_fname = nipraxis.fetch_file('ds114_sub009_t2r1_conv.txt')
regressor = np.loadtxt(conv_reg_fname)
plt.plot(regressor)

[<matplotlib.lines.Line2D at 0x7f30e8164430>]

Fetch and load the FMRI data, drop the first four volumes:

# Fetch.
bold_fname = nipraxis.fetch_file('ds114_sub009_t2r1.nii')
# Load
data = nib.load(bold_fname).get_fdata()
data = data[..., 4:]
print(data.shape)
n = data.shape[-1]

(64, 64, 30, 169)

Drop the matching time points in the regressor:

regressor = regressor[4:]

Make the design matrix for the simple regression:

X = np.ones((n, 2))
X[:, 1] = regressor
plt.imshow(X, cmap='gray', aspect=0.2)

<matplotlib.image.AxesImage at 0x7f30dff110f0>

Analysis on whole volume, reshaped

Reshape data to time by voxels:

Y = np.reshape(data, (-1, n))
Y = Y.T
Y.shape

(169, 122880)

Fit the design to the data:

\[ \newcommand{\yvec}{\vec{y}} \newcommand{\xvec}{\vec{x}} \newcommand{\evec}{\vec{\varepsilon}} \newcommand{Xmat}{\boldsymbol X} \newcommand{\bvec}{\vec{\beta}} \newcommand{\bhat}{\hat{\bvec}} \newcommand{\yhat}{\hat{\yvec}} \newcommand{\ehat}{\hat{\evec}} \newcommand{\cvec}{\vec{c}} \newcommand{\rank}{\textrm{rank}} \]

\[ \yvec = \Xmat \bvec + \evec \]

Here we calculate the fit for all the columns in in one shot - see Estimation for many voxels at the same time:

B = npl.pinv(X) @ Y
B.shape

(2, 122880)

Contrast to test the difference of the slope from 0:

c = np.array([0, 1])

Numerator of t test:

\[\begin{split} \newcommand{\cvec}{\vec{c}} \hat\sigma^2 = \frac{1}{n - \rank(\Xmat)} \sum e_i^2 \\ \end{split}\]

\[ t = \frac{\cvec^T \bhat} {\sqrt{\hat{\sigma}^2 \cvec^T (\Xmat^T \Xmat)^+ \cvec}} \]

top_of_t = c @ B
top_of_t.shape

(122880,)

This selected the second row of the B array:

np.all(top_of_t == B[1, :])

True

The denominator of the t statistic is given by the square root of two components:

• The estimated variance (from the squared residual errors in the data), multiplied by

• The covariance of the design - that depends only on the contrast and the design.

For the variance estimate, we need the degrees of freedom.

df_error = n - npl.matrix_rank(X)
df_error

167

fitted = X @ B
E = Y - fitted
E.shape

(169, 122880)

The denominator of the t statistic is the square root of the estimated variance, here called sigma_2, and the design correction, here called c_b_cov:

sigma_2 = np.sum(E ** 2, axis=0) / df_error
sigma_2

array([0., 0., 0., ..., 0., 0., 0.])

c_b_cov = c @ npl.pinv(X.T @ X) @ c
c_b_cov

0.023841202851645125

Here we left c as a 1D vector, and let the default of the @ matrix multiplication operator treat the 1D vector as a row vector on the left, and as a column vector on the right. See: Dot, vectors and matrices.

print(c)
print(c.shape)

[0 1]
(2,)

We could also make c into an explicit row vector to match the formula of the t statistic above. See Adding length 1 dimensions with newaxis.

c = c[:, None]
c.shape

(2, 1)

c_b_cov = c.T @ npl.pinv(X.T @ X) @ c
c_b_cov

array([[0.0238]])

Now we can have the parts that we need for the denominator, we can calculate the t statistic, one for each voxel:

t = top_of_t / np.sqrt(sigma_2 * c_b_cov)
t.shape

/tmp/ipykernel_5402/4169539846.py:1: RuntimeWarning: invalid value encountered in divide
  t = top_of_t / np.sqrt(sigma_2 * c_b_cov)

(1, 122880)

Reshape the 1D t statistic vector back into three dimensions to put the t statistic back into the correct voxel position:

t_3d = np.reshape(t, data.shape[:3])
print(t_3d.shape)
plt.imshow(t_3d[:, :, 15], cmap='gray')

(64, 64, 30)

<matplotlib.image.AxesImage at 0x7f30dff920e0>

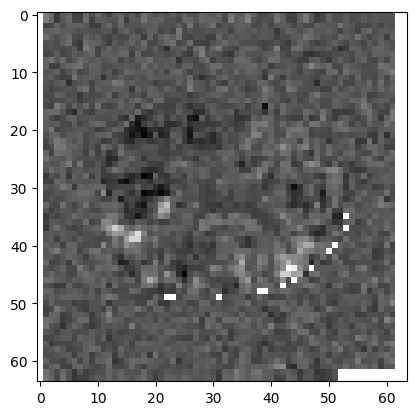
Notice the white areas at the edge of the image. These are voxels where the t value is nan – Not a number. See also Not a number. nan values arise when all the scans have 0 at this voxel, so the numerator and denominator of the t statistic are both 0.

np.array(0) / 0

/tmp/ipykernel_5402/2135315712.py:1: RuntimeWarning: invalid value encountered in divide
  np.array(0) / 0

nan

For example, this is the voxel corresponding to the top left corner of the image above:

t_3d[0, 0, 15]
np.all(data[0, 0, 15] == 0)

True

sigma_2_3d = np.reshape(sigma_2, data.shape[:3])
sigma_2_3d[0, 0, 15]

0.0

Can we avoid these uninteresting voxels, and only analyze voxels within the brain?

Analysis on voxels within the brain

Here we make a mask of the voxels within the brain using Otsu’s method. You will need scikit-image installed for this to work:

from skimage.filters import threshold_otsu
mean = np.mean(data, axis=-1)
mean.shape

(64, 64, 30)

thresh = threshold_otsu(mean)
thresh

849.7091461723373

# The mask has True for voxels above "thresh", False otherwise
mask = mean > thresh
mask.shape

(64, 64, 30)

plt.imshow(mask[:, :, 15], cmap='gray')
data.shape

(64, 64, 30, 169)

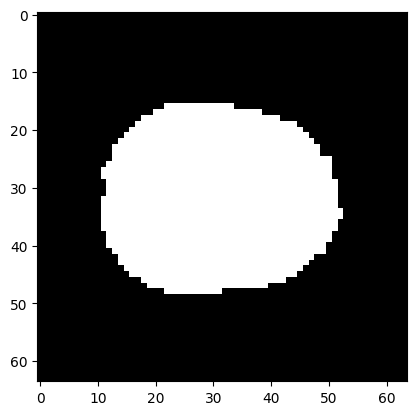
This is the number of voxels for which the mask value is True:

np.sum(mask)

21604

We can use the 3D mask to slice into the 4D data matrix. For every True value in the 3D mask, the result has the vector of values over time for that voxel. See: Indexing with Boolean masks.

Y = data[mask]
Y.shape

(21604, 169)

For our GLM, we want a time by in-mask voxel array, which is the transpose of the result above:

Y = data[mask].T
Y.shape

(169, 21604)

Now we can run our GLM on the voxels inside the brain:

B = npl.pinv(X) @ Y
fitted = X @ B
E = Y - fitted
sigma_2 = np.sum(E ** 2, axis=0) / df_error
# c and c_b_cov are the same as before, but recalculate anyway
c = np.array([0, 1])
c_b_cov = c @ npl.pinv(X.T @ X) @ c
t = c.T @ B / np.sqrt(sigma_2 * c_b_cov)
t.shape

(21604,)

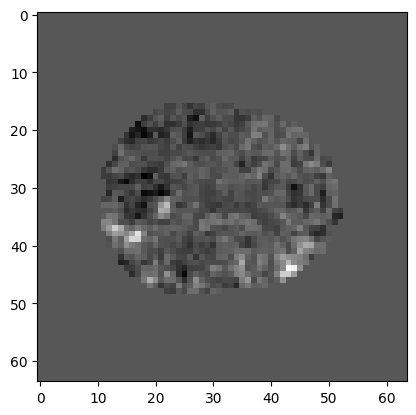
We can put the t values back into their correct positions in 3D by using the mask as an index on the left hand side:

t_3d = np.zeros(data.shape[:3])
t_3d[mask] = t
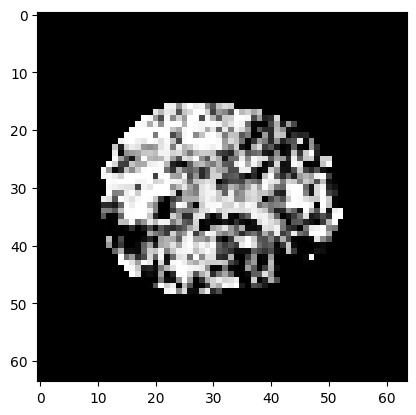
plt.imshow(t_3d[:, :, 15], cmap='gray')

<matplotlib.image.AxesImage at 0x7f30a5fe18a0>

Now we calculate the p value for each t statistic:

import scipy.stats as stats
t_dist = stats.t(df_error)
p = 1 - t_dist.cdf(t)
print(p.shape)
p_3d = np.zeros(data.shape[:3])
p_3d[mask] = p
plt.imshow(p_3d[:, :, 15], cmap='gray')

(21604,)

<matplotlib.image.AxesImage at 0x7f30ddd4fa60>

Multiple comparison correction

We now have a very large number of t statistics and p values. We want to find to control the family-wise error rate, where the “family” is the set of all of the voxel t tests / p values. See: Bonferroni correction. For reasons that you will in that page, the Bonferroni threshold is just the desired family-wise error rate (such as 0.05) divided by the number of voxels. This gives the single-voxel p value threshold at which we have a family-wise error rate of (e.g) 0.05.

N = p.shape[0]
bonferroni_thresh = 0.05 / N
bonferroni_thresh

2.31438622477319e-06

Binarize the voxel p values at the Bonferroni correction threshold, so voxels surviving correction have True, other voxels have False:

plt.imshow(p_3d[:, :, 15] < bonferroni_thresh, cmap='gray')

<matplotlib.image.AxesImage at 0x7f30e82c3610>

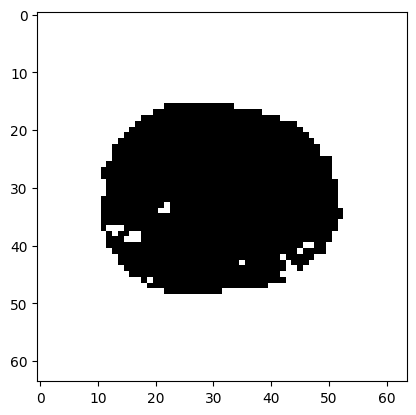
The voxels outside the brain have p value 0 (see above), so these always survive the correction above, and appear white.