Boolean indexing with more than one dimension

Boolean indexing with more than one dimension#

# import common modules
import numpy as np  # the Python array package
import matplotlib.pyplot as plt  # the Python plotting package

First we make a 3D array of shape (4, 3, 2), just as we did in the 3D array page:

# create an array of numbers from 0 to 11 inclusive, reshape this into a 4 rows by 3 columns array
plane0 = np.reshape(np.arange(12), (4, 3))
plane0

array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

# create an array of numbers from 100 to 111 inclusive, reshape this into a 4 rows by 3 columns array
plane1 = np.reshape(np.arange(100, 112), (4, 3))
plane1

array([[100, 101, 102],
       [103, 104, 105],
       [106, 107, 108],
       [109, 110, 111]])

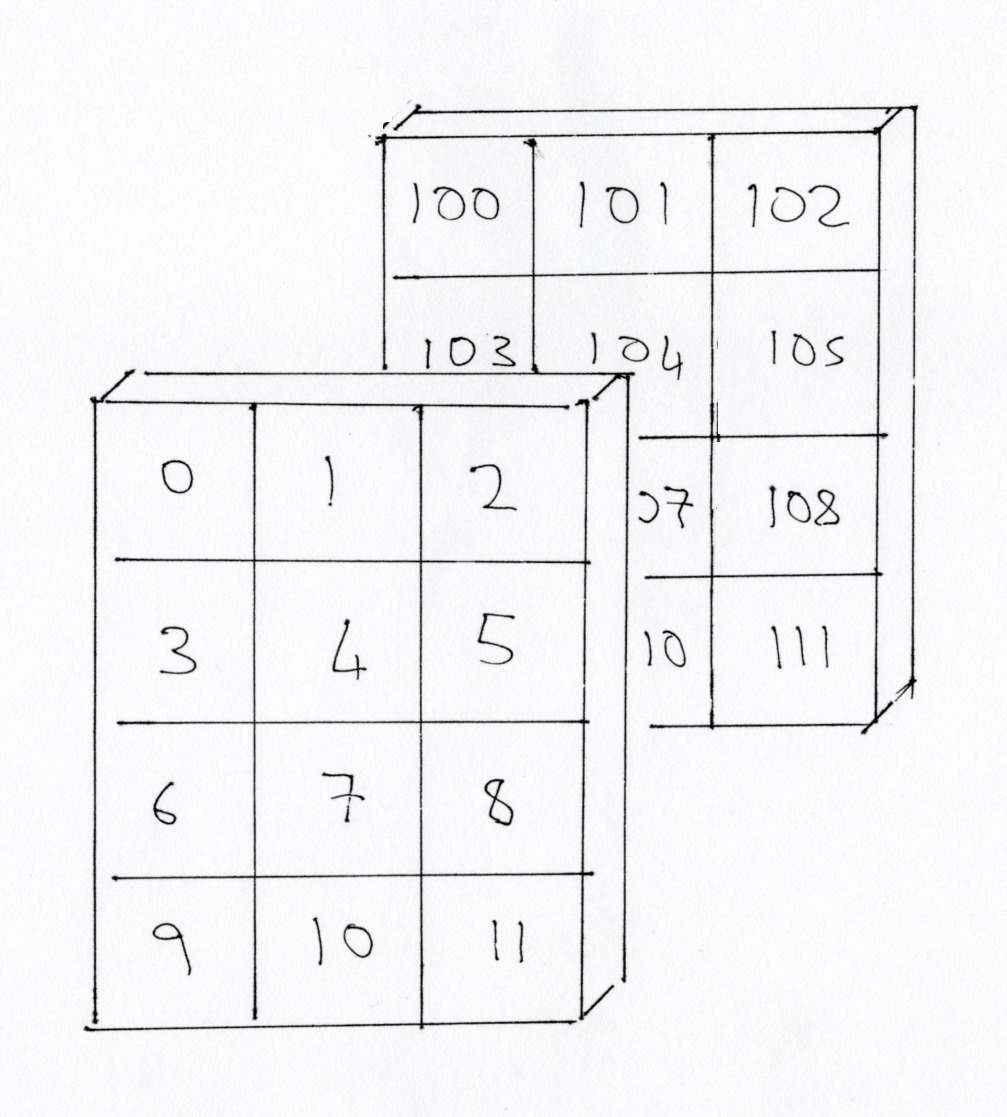
We can use np.stack to stack the two 2D arrays into a 3D array, by stacking over the third axis (axis=2):

# Make a 3D array by stacking the two 2D arrays.
arr_3d = np.stack([plane0, plane1], axis=2)
arr_3d

array([[[  0, 100],
        [  1, 101],
        [  2, 102]],

       [[  3, 103],
        [  4, 104],
        [  5, 105]],

       [[  6, 106],
        [  7, 107],
        [  8, 108]],

       [[  9, 109],
        [ 10, 110],
        [ 11, 111]]])

Here is the array pictured in 3D space:

Boolean indexing with more than one dimension#

Below you will see that we use Boolean arrays of one or two or three dimensions to index into a three-dimensional array.

This is a little hard to visualize, so we will go through it slowly. But first, we will give you the rule for what you get back from indexing with a Boolean array.

Let’s say you have an array A, of N dimensions - in our case N=3.

Let’s say you are indexing with a Boolean array B of P dimensions. P can be 1 or 2 or 3. Indexing A with B gives a result R, as in:

R = A[B]

Rule: The result R of Indexing an N-dimensional array A with a P-dimensional Boolean array B gives you one row for every True element in B, and as many extra dimension as are left in A — specifically, N - P. Let’s say there are T True elements in B. Then the shape of R is (T,) + A.shape[(N - P):]

That is a hard to follow in the abstract, but you will see the rule playing out in the examples below. We will rephrase the rule again a couple of times at the end.

Boolean indexing in two dimensions#

Let’s see how the rule plays out in two dimensions. Remember:

plane0

array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

Now imagine we index into this 2D array with a one-dimensional array:

B_1D = np.array([False, True, False, True])
B_1D

array([False,  True, False,  True])

res_1d = plane0[B_1D]
res_1d

array([[ 3,  4,  5],
       [ 9, 10, 11]])

Notice that the Boolean array B_1D has one element for each row in plane0, and it has selected only the rows of plane0 where there is a True in the Boolean array. There are 2 True values in B_1D (T, above = 2) B_1D has one dimension, leaving N - P = 2-1 = 1 dimension over, so the output array is two dimensions, shape (2,) + plane0.shape[1:] == (2, 3).

res_1d.shape

(2, 3)

Now lets try a two dimensional Boolean array.

B_2D = np.array([[True, False, True],
                 [False, True, False],
                 [True, False, True],
                 [True, True, False]])
B_2D

array([[ True, False,  True],
       [False,  True, False],
       [ True, False,  True],
       [ True,  True, False]])

res_2d = plane0[B_2D]
res_2d

array([ 0,  2,  4,  6,  8,  9, 10])

Notice that the Boolean array B_2D has one element for each element in plane0, and it has selected elements from plane0 where there is a True in the Boolean array. There are 7 True values in B_2D (T, above = 7) B_2D has two dimensions, leaving N - P = 2-2 = 0 dimension over, so the output array is one dimensions, shape (7,).

res_2d.shape

(7,)

Indexing a three-dimensional array with a 1D Boolean#

We can index arr_3d with a one-dimensional Boolean array. This selects elements from the first axis.

bool_1d = np.array([False, True, True, False])
arr_3d[bool_1d]

array([[[  3, 103],
        [  4, 104],
        [  5, 105]],

       [[  6, 106],
        [  7, 107],
        [  8, 108]]])

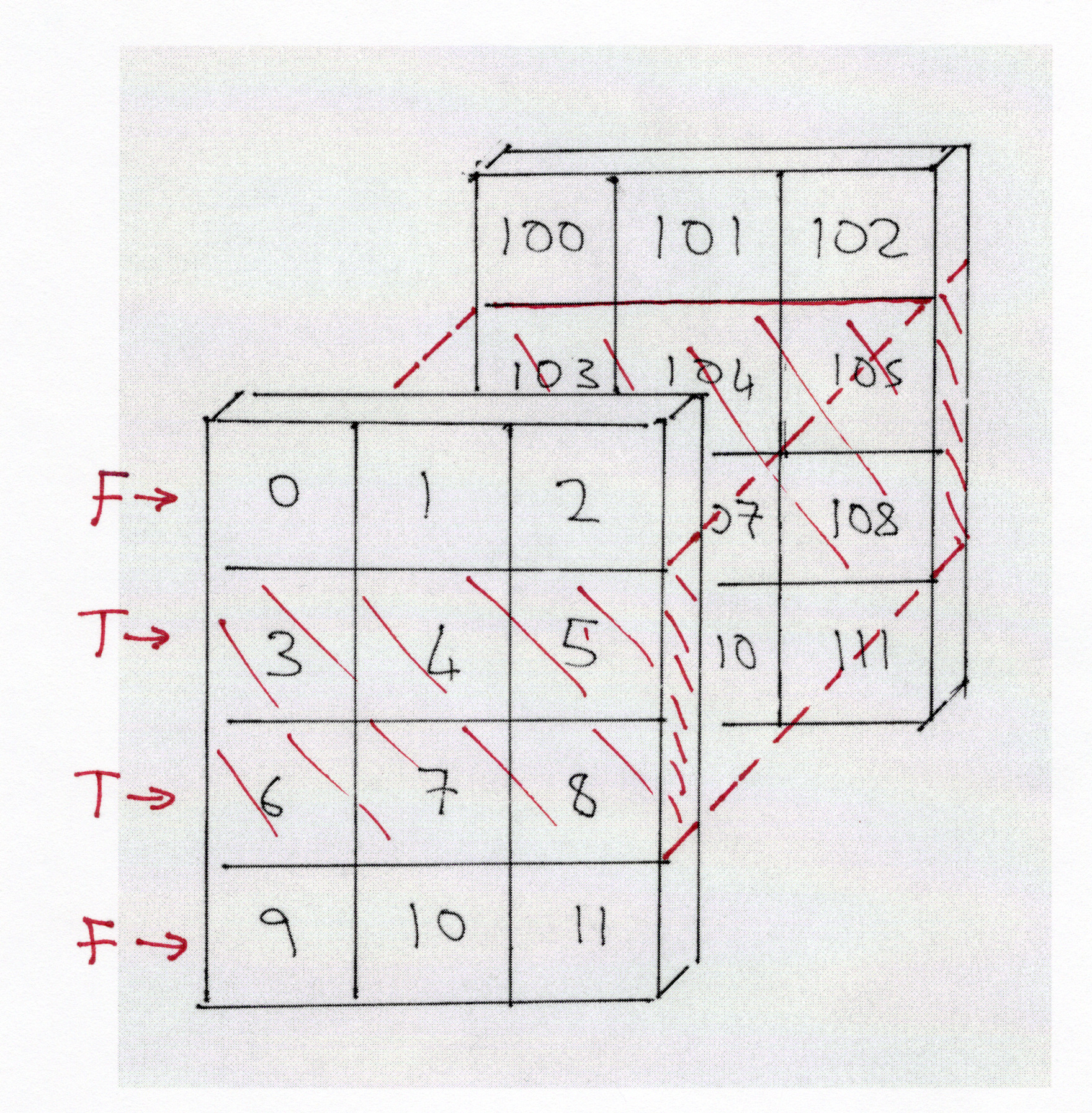
Pictured in 3D space, the first axis is the rows, across each plane. So, using [False, True, True, False] to index arr_3d is equivalent to stating “give me the 2nd and 3rd rows, across both remaining planes, from arr_3d”.

Put another way, the 1D Boolean index is saying, “Give me only the rows with True, and all the columns and all the planes”.

Remember that the True and False values in the Boolean array act as ‘switches’: only the elements corresponding to True make it into the final array:

# Show the final array, from indexing arr_3d with bool_1d
arr_3d[bool_1d]

array([[[  3, 103],
        [  4, 104],
        [  5, 105]],

       [[  6, 106],
        [  7, 107],
        [  8, 108]]])

Notice that the Boolean array bool_1d has one element for each row in arr_3d, and it has selected only the rows of arr_3d where there is a True in the Boolean array. There are 2 True values in bool_1D, T = 2, bool_1D has one dimension, leaving N - P = 3 - 1 = 2 dimensions over, so the output array is three dimensions, shape (2,) + arr_3d.shape[1:] == (2, 3, 2).

# Show the shape of the final array.
arr_3d[bool_1d].shape

(2, 3, 2)

Indexing a three-dimensional array with a 2D Boolean#

We can also index with a two-dimensional Boolean array.

Put another way, we want “Only the rows, columns with a True value, and all the planes”.

bool_2d = np.array([[False, True, False],
                    [True, False, True],
                    [True, False, False],
                    [False, False, True],
                   ])
bool_2d

array([[False,  True, False],
       [ True, False,  True],
       [ True, False, False],
       [False, False,  True]])

If we index with this array, it selects elements from the first two axes.

Put another way, we want “Only the rows, columns with a True value, and all the planes”.

# index arr_3d with bool_2d
arr_3d[bool_2d]

array([[  1, 101],
       [  3, 103],
       [  5, 105],
       [  6, 106],
       [ 11, 111]])

You can think of the bool_2d array as ‘switching’ on or off individual columns of the arr_3d array. If we show this as a sequence, pictured in 3D space, it looks as follows:

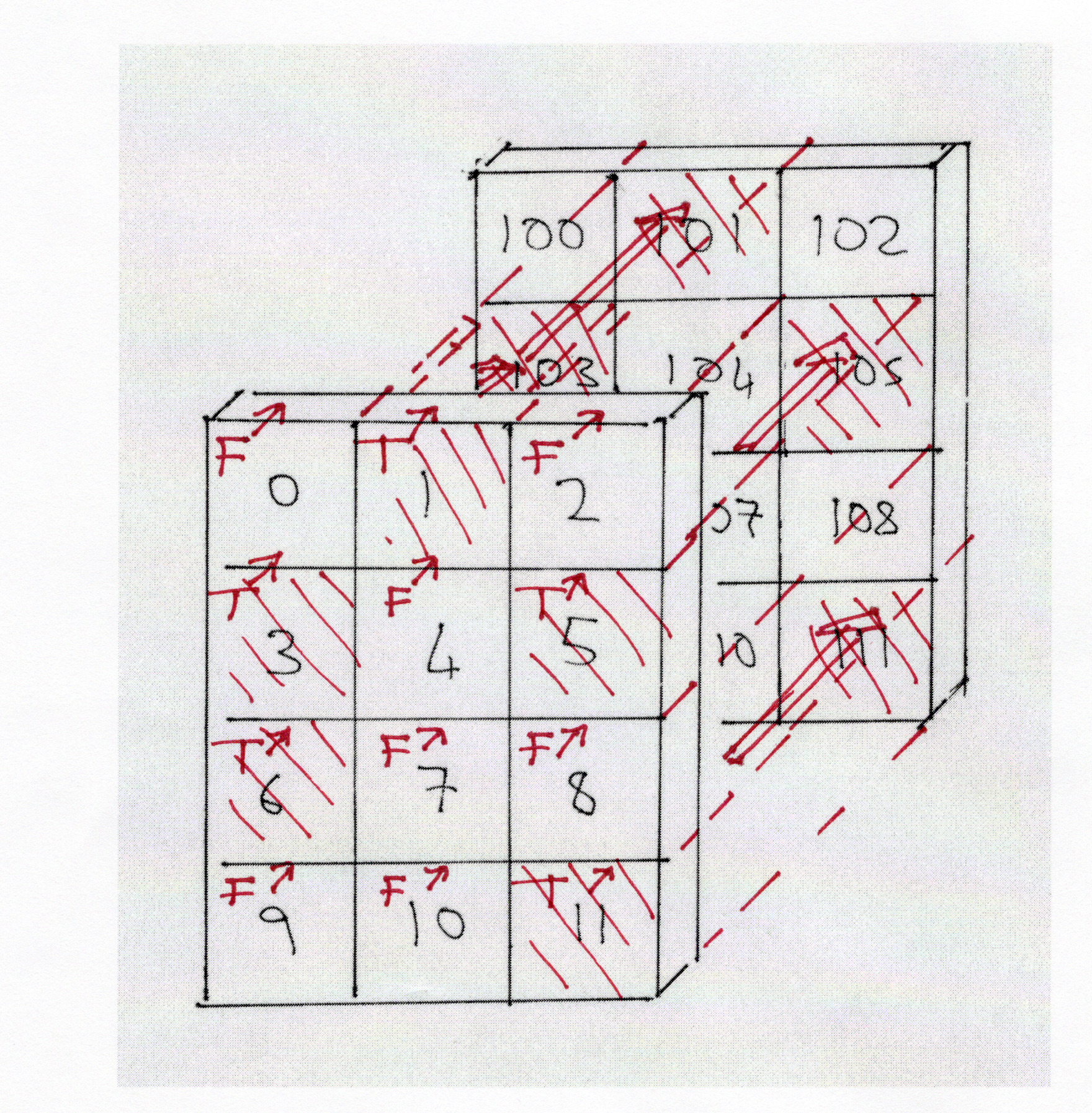
In this case, using bool_2d to index arr_3d yields an array with one plane, with 5 rows and 2 columns:

arr_3d[bool_2d]

array([[  1, 101],
       [  3, 103],
       [  5, 105],
       [  6, 106],
       [ 11, 111]])

The Boolean array bool_2d has one element for each row, column pair in arr_3d, and it has selected only the row, column pairs of arr_3d where there is a True in the Boolean array. There are 5 True values in bool_2d, T = 5, bool_2d has two dimensions, leaving N - P = 3 - 2 = 1 dimensions left over, so the output array is two dimensions, shape (5,) + arr_3d.shape[2:] == (5, 2).

# show the shape of the arr_3d array, when indexed with the bool_2d boolean array
arr_3d[bool_2d].shape

(5, 2)

Indexing a three-dimensional array with a 3D Boolean#

We can even index with a 3D array, this selects elements over all three dimensions. In which order does it get the elements?

# A zero (=False) array of all Booleans (dtype=bool)
bool_3d = np.zeros((4, 3, 2), dtype=bool)
bool_3d

array([[[False, False],
        [False, False],
        [False, False]],

       [[False, False],
        [False, False],
        [False, False]],

       [[False, False],
        [False, False],
        [False, False]],

       [[False, False],
        [False, False],
        [False, False]]])

# Fill in the first plane with the original 2D array
bool_3d[:, :, 0] = bool_2d
# Fill in the second plane with another 2D array.
another_bool_2d = np.array([[True, True, False],
                            [False, False, False],
                            [True, True, False],
                            [True, False, False],
                           ])
bool_3d[:, :, 1] = another_bool_2d
bool_3d

array([[[False,  True],
        [ True,  True],
        [False, False]],

       [[ True, False],
        [False, False],
        [ True, False]],

       [[ True,  True],
        [False,  True],
        [False, False]],

       [[False,  True],
        [False, False],
        [ True, False]]])

# Use bool_3d to index arr_3d
arr_3d[bool_3d]

array([100,   1, 101,   3,   5,   6, 106, 107, 109,  11])

The Boolean array bool_3d has one element for each row, column, plane triple in arr_3d. Each triple defines an element. bool_3d has selected only the elements of arr_3d where there is a True in the Boolean array. There are 10 True values in bool_3d.

np.count_nonzero(bool_3d)

Therefore T = 10, bool_3d has three dimensions leaving N - P = 3 - 3 = 0 dimensions left over, so the output array is one dimension, shape (10,).

# Show the shape
arr_3d[bool_3d].shape

(10,)

Another summary of the rule#

Now we have done the indexing in one, two and three dimensions, let us think again about the rule for the shape.

The Boolean index selects the items on the corresponding dimension(s). Therefore:

A 1D index on its own selects rows (and leaves columns and planes intact). The output has one row for each True in the array, and the original number of columns and planes. It is therefore 3D.
A 2D index on its own selects row, column elements (and leaves planes intact). The output has one row for each True in the 2D array (each selected row, column pair), and the original number of planes. It is therefore 2D.
A 3D index selects row, column, plane elements. The output has one row for each True in the 3D array (each selected row, column, plane element). It is therefore 1D.

What’s the rule again?

The dimensions in the indexing Boolean array get collapsed to a single dimension. Call that the Boolean dimension. The dimension has the same number of elements are there are True values in the Boolean array. The remaining dimensions persist. In our case:

1D Boolean collapses the single dimension to a single dimension - giving Boolean dimension x columns x planes.
2D Boolean collapses two dimensions to a single dimension - giving Boolean dimension x planes.
3D Boolean collapses all three dimensions to a single dimension - giving Boolean dimension.

In each of the cases above, the Boolean dimension has the same length as the number of True elements in the indexing Boolean array.

Using 1D Boolean arrays on other axes#

We can also mix 1D Boolean arrays with ordinary slicing to select elements on a single axis. E.g. the code below returns the entire second plane of arr_3d:

bool_1d_dim3 = np.array([False, True])
arr_3d[:, :, bool_1d_dim3]

array([[[100],
        [101],
        [102]],

       [[103],
        [104],
        [105]],

       [[106],
        [107],
        [108]],

       [[109],
        [110],
        [111]]])

Boolean indexing with more than one dimension

Contents

Boolean indexing with more than one dimension#

Boolean indexing with more than one dimension#

Boolean indexing in two dimensions#

Indexing a three-dimensional array with a 1D Boolean#

Indexing a three-dimensional array with a 2D Boolean#

Indexing a three-dimensional array with a 3D Boolean#

Another summary of the rule#

Using 1D Boolean arrays on other axes#