Voxels and time

See also: Reshaping, 4D to 2D.

# Import common modules
import numpy as np  # the Python array package
import matplotlib.pyplot as plt  # the Python plotting package
# Display array values to 6 digits of precision
np.set_printoptions(precision=4, suppress=True)

In this example, we calculate the mean across all voxels at each time point.

We’re working on ds114_sub009_t2r1.nii. This is a 4D FMRI image.

import nipraxis
bold_fname = nipraxis.fetch_file('ds114_sub009_t2r1.nii')
bold_fname

'/home/runner/.cache/nipraxis/0.5/ds114_sub009_t2r1.nii'

import nibabel as nib
img = nib.load(bold_fname)
img.shape

(64, 64, 30, 173)

We want to calculate the mean across all voxels. Remember that a voxel is a pixel with volume, and refers to a position in space. Therefore we have this number of voxels in each volume:

n_voxels = np.prod(img.shape[:-1])
n_voxels

122880

To calculate the mean across all voxels, for a single volume, we can do this:

data = img.get_fdata()
first_vol = data[..., 0]
np.mean(first_vol)

414.40107421875

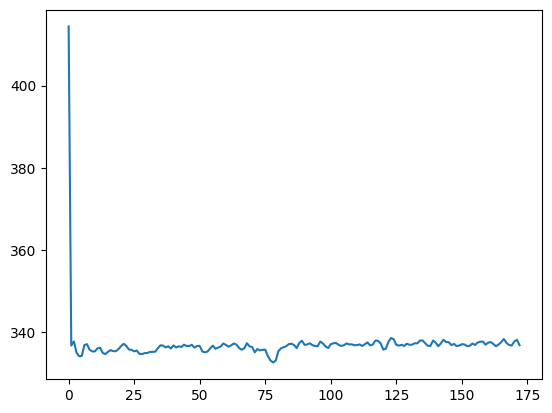
To calculate the mean across voxels, we could loop across all volumes, and calculate the mean for each volume:

n_trs = img.shape[-1]
means = []
for vol_no in range(n_trs):
    vol = data[..., vol_no]
    means.append(np.mean(vol))

plt.plot(means)

[<matplotlib.lines.Line2D at 0x7fef28150a60>]

We could also flatten the three voxel axes out into one long voxel axis, using reshape – see: Reshaping, 4D to 2D. Then we can use the axis parameter to the np.mean function to calculate the mean across voxels, in one shot. This is “vectorizing”, where we take an operation that needed a loop, and use array operations to do the work instead:

voxels_by_time = np.reshape(data, (n_voxels, n_trs))
means_vectorized = np.mean(voxels_by_time, axis=0)
# The answer is the same, allowing for tiny variations.
assert np.allclose(means_vectorized, means)