Introduction to the general linear model#
For more detail on the General Linear Model, see The general linear model and fMRI: Does love last forever?.
# Import numerical and plotting libraries
import numpy as np
import numpy.linalg as npl
import matplotlib.pyplot as plt
# Only show 6 decimals when printing
np.set_printoptions(precision=6)
This page starts with the model for simple regression, that you have already seen in the regression page, and in regression notation. We then show how the simple regression gets expressed in a design matrix. Once we have that, it’s easy to extend simple regression to multiple regression. By adding some specially formed regressors, we can also express group membership, and therefore do ANalysis Of VAriance (ANOVA). This last step is where multiple regression becomes the General Linear Model (GLM).
Simple regression#
You have already seen this problem in the regression page.
We have measured scores for a “psychopathy” personality trait in 12 students. We also measured how much sweat each student had on their palms, and we call this a “clammy” score. We will look for a straight-line (linear) relationship between the “clammy” score (our predictor or regressor) and the “psychopathy” score (our predicted variable).
# The values we are trying to predict.
psychopathy = np.array(
[11.416, 4.514, 12.204, 14.835,
8.416, 6.563, 17.343, 13.02,
15.19 , 11.902, 22.721, 22.324])
# The values we will predict with.
clammy = np.array(
[0.389, 0.2 , 0.241, 0.463,
4.585, 1.097, 1.642, 4.972,
7.957, 5.585, 5.527, 6.964])
# The number of values
n = len(clammy)
plt.plot(clammy, psychopathy, '+')
plt.xlabel('Clamminess of handshake')
plt.ylabel('Psychopathy score')
Text(0, 0.5, 'Psychopathy score')
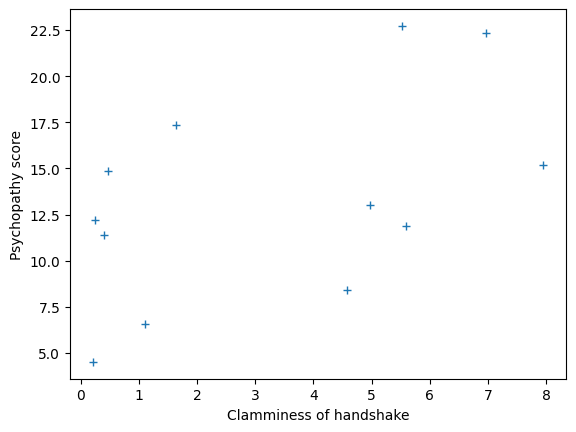
Let’s immediately rename the values we are predicting to y, and the values we are predicting with to x:
y = psychopathy
x = clammy
You have already seen a preliminary guess we made at a straight line that links
the clammy scores to the psychopathy scores. Our guess was:
b = 0.9
c = 10
We use this line to predict the psychopathy scores from the clammy scores.
predicted = b * clammy + c
predicted
array([10.3501, 10.18 , 10.2169, 10.4167, 14.1265, 10.9873, 11.4778,
14.4748, 17.1613, 15.0265, 14.9743, 16.2676])
# Plot the data and the predictions
plt.plot(x, y, '+', label='Actual data')
plt.plot(x, predicted, 'ro', label='Predictions')
plt.xlabel('Clamminess of handshake')
plt.ylabel('Psychopathy score')
plt.title('Clammy vs psychopathy with guessed line')
plt.legend()
<matplotlib.legend.Legend at 0x7f70e421d360>
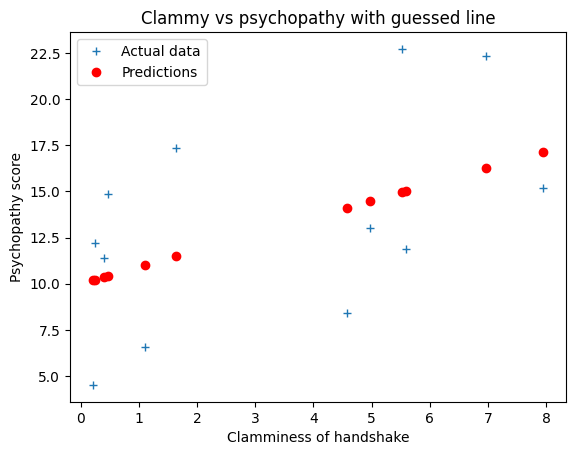
As you saw in regression notation, we can write out this model more formally and more generally in mathematical symbols.
\(\newcommand{\yvec}{\vec{y}} \newcommand{\xvec}{\vec{x}} \newcommand{\evec}{\vec{\varepsilon}}\)
We write our y (psychopathy) data \(\yvec\) — a vector with 12 values, one
for each student.
\(y_1\) is the value for the first student (= 11.416) and \(y_i\) is the value for student \(i\) where \(i \in 1 .. 12\):
Show code cell source
# Ignore this cell - it is to give a better display to the mathematics.
# Import Symbolic mathematics routines.
from sympy import Eq, Matrix, IndexedBase, symbols, init_printing
from sympy.matrices import MatAdd, MatMul, MatrixSymbol
# Make equations print in definition order.
init_printing(order='none')
sy_y = symbols(r'\vec{y}')
sy_y_ind = IndexedBase("y")
vector_indices = range(1, n + 1)
sy_y_val = Matrix([sy_y_ind[i] for i in vector_indices])
Eq(sy_y, Eq(sy_y_val, Matrix(y)), evaluate=False)
x (the clammy score) is a predictor. Lets call the clammy scores \(\xvec\).
\(\xvec\) is another vector with 12 values. \(x_1\) is the value for the first
student (= 0.389) and \(x_i\) is the value for student \(i\) where \(i \in 1 .. 12\).
Show code cell source
# Ignore this cell - it is to give a better display to the mathematics.
sy_x = symbols(r'\vec{x}')
sy_x_ind = IndexedBase("x")
sy_x_val = Matrix([sy_x_ind[i] for i in vector_indices])
Eq(sy_x, Eq(sy_x_val, Matrix(x)), evaluate=False)
In regression notation, we wrote our straight line model as:
\(y_i = bx_i + c + e_i\)
Simple regression in matrix form#
It turns out it will be useful to rephrase the simple regression model in matrix form. Let’s make the data and predictor and errors into vectors.
We already the \(y\) values in our \(\yvec\) vector above, and the \(x\) values in the \(\xvec\) vector.
\(\evec\) is the vector of as-yet-unknown errors \(e_1, e_2, ... e_{12}\). The values of the errors depend on the predicted values, and therefore, on our slope \(b\) and intercept \(c\).
We calculate the errors as:
e = y - predicted
We write the errors as an error vector:
Show code cell source
# Ignore this cell.
sy_e = symbols(r'\vec{\varepsilon}')
sy_e_ind = IndexedBase("e")
sy_e_val = Matrix([sy_e_ind[i] for i in vector_indices])
Eq(sy_e, sy_e_val, evaluate=False)
Now we can rephrase our model as:
Show code cell source
# Ignore this cell.
sy_b, sy_c = symbols('b, c')
sy_c_mat = MatrixSymbol('c', 12, 1)
rhs = MatAdd(MatMul(sy_b, sy_x_val), sy_c_mat, sy_e_val)
Eq(sy_y_val, rhs, evaluate=False)
Confirm this is true when we calculate on our particular values:
# Confirm that y is close as dammit to b * x + c + e
assert np.allclose(y, b * x + c + e)
Bear with with us for a little trick. We define \(\vec{o}\) as a vector of ones, like this:
Show code cell source
# Ignore this cell.
sy_o = symbols(r'\vec{o}')
sy_o_val = Matrix([1 for i in vector_indices])
Eq(sy_o, sy_o_val, evaluate=False)
In code, in our case:
o = np.ones(n)
Now we can rewrite the formula as:
because \(o_i = 1\) and so \(co_i = c\).
Show code cell source
# Ignore this cell.
rhs = MatAdd(MatMul(sy_b, sy_x_val), MatMul(sy_c, sy_o_val), sy_e_val)
Eq(sy_y_val, rhs, evaluate=False)
This evaluates to the result we intend:
Show code cell source
# Ignore this cell.
Eq(sy_y_val, sy_c * sy_o_val + sy_b * sy_x_val + sy_e_val, evaluate=False)
# Confirm that y is close as dammit to b * x + c * o + e
assert np.allclose(y, b * x + c * o + e)
\(\newcommand{Xmat}{\boldsymbol X} \newcommand{\bvec}{\vec{\beta}}\)
We can now rephrase the calculation in terms of matrix multiplication.
Call \(\Xmat\) the matrix of two columns, where the first column is \(\xvec\) and the second column is the column of ones (\(\vec{o}\) above).
In code, for our case:
X = np.stack([x, o], axis=1)
X
array([[0.389, 1. ],
[0.2 , 1. ],
[0.241, 1. ],
[0.463, 1. ],
[4.585, 1. ],
[1.097, 1. ],
[1.642, 1. ],
[4.972, 1. ],
[7.957, 1. ],
[5.585, 1. ],
[5.527, 1. ],
[6.964, 1. ]])
Call \(\bvec\) the column vector:
In code:
B = np.array([b, c])
B
array([ 0.9, 10. ])
This gives us exactly the same calculation as \(\yvec = b \xvec + c + \evec\) above, but in terms of matrix multiplication:
Show code cell source
# Ignore this cell.
sy_beta_val = Matrix([[sy_b], [sy_c]])
sy_xmat_val = Matrix.hstack(sy_x_val, sy_o_val)
Eq(sy_y_val, MatAdd(MatMul(sy_xmat_val, sy_beta_val), sy_e_val), evaluate=False)
In symbols:
Because of the way that matrix multiplication works, this again gives us the intended result:
Show code cell source
# Ignore this cell.
Eq(sy_y_val, sy_xmat_val @ sy_beta_val + sy_e_val, evaluate=False)
We write matrix multiplication in Numpy as @:
# Confirm that y is close as dammit to X @ B + e
assert np.allclose(y, X @ B + e)
We still haven’t found our best fitting line. But before we go further, it might be clear that we can easily add a new predictor here.
Multiple regression#
Let’s say we think that psychopathy increases with age. We add the student’s age as another predictor:
age = np.array(
[22.5, 25.3, 24.6, 21.4,
20.7, 23.3, 23.8, 21.7,
21.3, 25.2, 24.6, 21.8])
Now rename the clammy predictor vector from \(\xvec\) to
\(\xvec_1\).
# clammy (our previous x) is the first column we will use to predict.
x_1 = clammy
Of course \(\xvec_1\) has 12 values \(x_{1, 1}..x_{1, 12}\). Call the age
predictor vector \(\xvec_2\).
# age is the second column we use to predict
x_2 = age
Call the slope for clammy \(b_1\) (slope for \(\xvec_1\)). Call the slope for age
\(b_2\) (slope for \(\xvec_2\)). Our model is:
Show code cell source
# Ignore this cell.
sy_b_1, sy_b_2 = symbols('b_1, b_2')
sy_x_1_ind = IndexedBase("x_1,")
sy_x_1_val = Matrix([sy_x_1_ind[i] for i in vector_indices])
sy_x_2_ind = IndexedBase("x_2,")
sy_x_2_val = Matrix([sy_x_2_ind[i] for i in vector_indices])
Eq(sy_y_val, MatAdd(MatMul(sy_b_1, sy_x_1_val), MatMul(sy_b_2, sy_x_2_val), sy_c_mat, sy_e_val), evaluate=False)
In this model \(\Xmat\) has three columns (\(\xvec_1\), \(\xvec_2\) and ones), and the \(\bvec\) vector has three values \(b_1, b_2, c\). This gives the same matrix formulation, with our new \(\Xmat\) and \(\bvec\): \(\yvec = \Xmat \bvec + \evec\).
This is a linear model because our model says that the data \(y_i\) comes from the sum of some components (\(b_1 x_{1, i}, b_2 x_{2, i}, c, e_i\)).
We can keep doing this by adding more and more regressors. In general, a linear model with \(p\) predictors looks like this:
In the case of the models above, the final predictor \(\xvec_p\) would be a column of ones, to express the intercept in the model.
Any model of the form above can still be phrased in the matrix form:
where:
Show code cell source
# Ignore this cell.
sy_xmat3_val = Matrix.hstack(sy_x_1_val, sy_x_2_val, sy_o_val)
sy_Xmat = symbols(r'\boldsymbol{X}')
Eq(sy_Xmat, sy_xmat3_val, evaluate=False)
In code in our case:
# Design X in values
X_3_cols = np.stack([x_1, x_2, o], axis=1)
X_3_cols
array([[ 0.389, 22.5 , 1. ],
[ 0.2 , 25.3 , 1. ],
[ 0.241, 24.6 , 1. ],
[ 0.463, 21.4 , 1. ],
[ 4.585, 20.7 , 1. ],
[ 1.097, 23.3 , 1. ],
[ 1.642, 23.8 , 1. ],
[ 4.972, 21.7 , 1. ],
[ 7.957, 21.3 , 1. ],
[ 5.585, 25.2 , 1. ],
[ 5.527, 24.6 , 1. ],
[ 6.964, 21.8 , 1. ]])
In symbols:
Show code cell source
# Ignore this cell.
sy_beta2_val = Matrix([sy_b_1, sy_b_2, sy_c])
Eq(sy_y_val, MatAdd(MatMul(sy_xmat3_val, sy_beta2_val), sy_e_val), evaluate=False)
As we were hoping, this evaluates to:
Show code cell source
# Ignore this cell.
Eq(sy_y_val, sy_xmat3_val @ sy_beta2_val + sy_e_val, evaluate=False)
Population, sample, estimate#
\(\newcommand{\bhat}{\hat{\bvec}} \newcommand{\yhat}{\hat{\yvec}}\) Our students and their psychopathy scores are a sample from the population of all students’ psychopathy scores. The parameters \(\bvec\) are the parameters that fit the design \(\Xmat\) to the population scores. We only have a sample from this population, so we cannot get the true population \(\bvec\) vector, we can only estimate \(\bvec\) from our sample. We will write this sample estimate as \(\bhat\) to distinguish it from the true population parameters \(\bvec\).
Solving the model with matrix algebra#
The reason to formulate our problem with matrices is so we can use some basic matrix algebra to estimate the “best” line.
Let’s assume that we want an estimate for the line parameters (intercept and slope) that gives the smallest “distance” between the estimated values (predicted from the line), and the actual values (the data).
We’ll define ‘distance’ as the squared difference of the predicted value from the actual value. These are the squared error terms \(e_1^2, e_2^2 ... e_{n}^2\), where \(n\) is the number of observations; 12 in our case.
As a reminder: our model is:
Where \(\yvec\) is the data vector \(y_1, y_2, ... y_n\), \(\Xmat\) is the design matrix of shape \(n, p\), \(\bvec\) is the parameter vector, \(b_1, b_2 ... b_p\), and \(\evec\) is the error vector giving errors for each observation \(\epsilon_1, \epsilon_2 ... \epsilon_n\).
Each column of \(\Xmat\) is a regressor vector, so \(\Xmat\) can be thought of as the column concatenation of \(p\) vectors \(\xvec_1, \xvec_2 ... \xvec_p\), where \(\xvec_1\) is the first regressor vector, and so on.
In our case, we want an estimate \(\bhat\) for the vector \(\bvec\) such that the errors \(\evec = \yvec - \Xmat \bhat\) have the smallest sum of squares \(\sum_{i=1}^n{e_i^2}\). \(\sum_{i=1}^n{e_i^2}\) is called the residual sum of squares.
When we have our \(\bhat\) estimate, then the prediction of the data from the estimate is given by \(\Xmat \bhat\).
We call this the predicted or estimated data, and write it as \(\yhat\). The errors are then given by \(\yvec - \yhat\).
We might expect that, when we have found the right \(\bhat\) then the errors will have nothing in them that can still be explained by the design matrix \(\Xmat\). This is the same as saying that, when we have best prediction of the data (\(\yhat = \Xmat \bhat\)), the design matrix \(\Xmat\) should be orthogonal to the remaining error (\(\yvec - \yhat\)).
For those of you who have learned about vectors in mathematics, you may remember that we say that two vectors are orthogonal if they have a dot product of zero.
If the design is orthogonal to the errors, then \(\Xmat^T \evec\) should be a vector of zeros.
If that is the case then we can multiply \(\yvec = \Xmat \bhat + \evec\) through by \(\Xmat^T\):
The last term now disappears because it is zero and:
If \(\Xmat^T \Xmat\) is invertible (has a matrix inverse \((\Xmat^T \Xmat)^{-1}\)) then there is a unique solution:
It turns out that, if \(\Xmat^T \Xmat\) is not invertible, there are an infinite number of solutions, and we have to choose one solution, taking into account that the parameters \(\bhat\) will depend on which solution we chose. The pseudoinverse operator gives us one particular solution. If \(\bf{A}^+\) is the pseudoinverse of matrix \(\bf{A}\) then the general solution for \(\bhat\), even when \(\Xmat^T \Xmat\) is not invertible, is:
Using this matrix algebra, what line do we estimate for psychopathy
and clammy?
X = np.column_stack((clammy, np.ones(12)))
X
array([[0.389, 1. ],
[0.2 , 1. ],
[0.241, 1. ],
[0.463, 1. ],
[4.585, 1. ],
[1.097, 1. ],
[1.642, 1. ],
[4.972, 1. ],
[7.957, 1. ],
[5.585, 1. ],
[5.527, 1. ],
[6.964, 1. ]])
# Use the pseudoinverse to get estimated B
B = npl.pinv(X) @ psychopathy
B
array([ 0.999257, 10.071286])
# Plot the data
plt.plot(clammy, psychopathy, '+')
[<matplotlib.lines.Line2D at 0x7f70c997a2f0>]
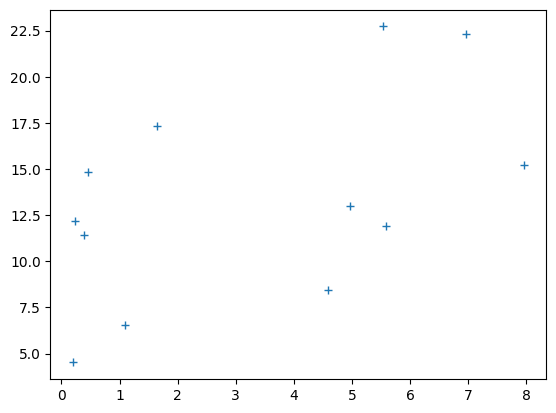
best_slope = B[0]
best_intercept = B[1]
best_predictions = best_intercept + best_slope * clammy
# Plot the new prediction
plt.plot(clammy, psychopathy, '+', label='Actual data')
plt.plot(clammy, best_predictions, 'ro', label='Best predictions')
plt.xlabel('Clamminess of handshake')
plt.ylabel('Psychopathy score')
plt.title('Clammy vs psychopathy with best line')
plt.legend();
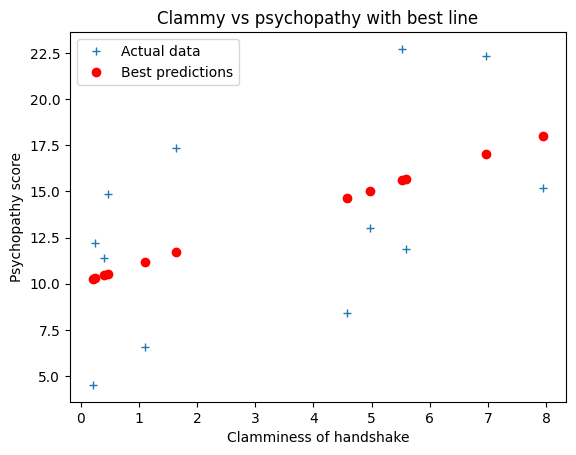
Our claim was that this estimate for slope and intercept minimize the sum (and therefore mean) of squared error:
fitted = X @ B
errors = psychopathy - fitted
print(np.sum(errors ** 2))
252.92560644993824
Is this sum of squared errors smaller than our earlier guess of an intercept of 10 and a slope of 0.9?
fitted = X @ [0.9, 10]
errors = psychopathy - fitted
print(np.sum(errors ** 2))
255.75076072
Contrasts#
\(\newcommand{cvec}{\mathbf{c}}\) We can combine the values in the \(\bhat\) vector in different ways by using a contrast vector. A contrast vector \(\cvec\) is a vector of weights \(c_1, c_2 ... c_p\) for each value in the \(\bhat\) vector. Assume that all vectors we have defined up until now are column vectors. Then a scalar value that is a linear combination of the \(\bhat\) values can be written:
We now return to our original question, whether clamminess of handshake predicts psychopathy score.
If clamminess does predict psychopathy, then we would expect the slope
of the best fit line between clammy and psychopathy would be
different from zero.
In our model, we have two predictors, the column of ones and clammy.
\(p = 2\) and \(\bhat\) is length 2. We could choose just the first of
the values in \(\bhat\) with a contrast:
\(\cvec^T \bhat\) with this contrast gives our estimate of the
slope relating clammy to psychopathy. Now we might be interested
if our estimate is further from zero than expected by chance.
To test whether the estimate is different from zero, we can divide the estimate by the variability of the estimate. This gives us an idea of how far the estimate is from zero, in terms of the variability of the estimate. We won’t go into the estimate of the variability here though, we’ll just assume it (the formula is in the code below). The estimate divided by the variability of the estimate gives us a t statistic.
With that introduction, here’s how to do the estimation and a t statistic given the data \(\yvec\), the design \(\Xmat\), and a contrast vector \(\cvec\).
# Get t distribution code from scipy library
from scipy.stats import t as t_dist
def t_stat(y, X, c):
""" betas, t statistic and significance test given data, design matrix, contrast
This is Ordinary Least Square estimation; we assume the errors to have
independent and identical normal distributions around zero for each $i$ in
$\e_i$ (i.i.d).
"""
# Make sure y, X, c are all arrays
y = np.asarray(y)
X = np.asarray(X)
c = np.atleast_2d(c).T # As column vector
# Calculate the parameters - b hat
beta = npl.pinv(X) @ y
# The fitted values - y hat
fitted = X @ beta
# Residual error
errors = y - fitted
# Residual sum of squares
RSS = np.sum(errors**2, axis=0)
# Degrees of freedom is the number of observations n minus the number
# of independent regressors we have used. If all the regressor
# columns in X are independent then the (matrix rank of X) == p
# (where p the number of columns in X). If there is one column that
# can be expressed as a linear sum of the other columns then
# (matrix rank of X) will be p - 1 - and so on.
df = X.shape[0] - npl.matrix_rank(X)
# Mean residual sum of squares
MRSS = RSS / df
# calculate bottom half of t statistic
SE = np.sqrt(MRSS * c.T @ npl.pinv(X.T @ X) @ c)
t = c.T @ beta / SE
# Get p value for t value using cumulative density function
# (CDF) of the t distribution.
ltp = t_dist.cdf(t, df) # lower tail p
p = 1 - ltp # upper tail p
return beta, t, df, p
See p values from cumulative distribution functions for background on the probability values.
So, does clammy predict psychopathy? If it does not, then our
estimate of the slope will not be convincingly different from 0. The t
test divides our estimate of the slope by the error in the estimate;
large values mean that the slope is large compared to the error in the
estimate.
X = np.column_stack((clammy, np.ones(12)))
Y = np.asarray(psychopathy)
B, t, df, p = t_stat(Y, X, [1, 0])
t, p
(array([[1.914389]]), array([[0.042295]]))
Dummy coding and the general linear model#
So far we have been doing multiple regression. That is, all the columns
(except the column of ones) are continuous vectors of numbers predicting our
outcome data psychopathy. These type of predictors are often called
covariates.
It turns out we can use this same framework to express the fact that different observations come from different groups.
Expressing group membership in this way allows us to express analysis of variance designs using this same notation.
To do this, we use columns of dummy variables.
Let’s say we get some new and interesting information. The first 4 students come from Berkeley, the second set of 4 come from Stanford, and the last set of 4 come from MIT. Maybe the student’s college predicts if they are a psychopath?
How do we express this information? Let’s forget about the clamminess score for now and just use the school information. Our model might be that we can best predict the psychopathy scores by approximating the individual student psychopathy scores with a mean score for the relevant school:
We can code this with predictors in our design using indicator variables. The “Berkeley” indicator variable vector is 1 when the student is from Berkeley and zero otherwise. Similarly for the other two schools:
berkeley_indicator = [1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
stanford_indicator = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0]
mit_indicator = [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1]
X = np.column_stack((berkeley_indicator,
stanford_indicator,
mit_indicator))
X
array([[1, 0, 0],
[1, 0, 0],
[1, 0, 0],
[1, 0, 0],
[0, 1, 0],
[0, 1, 0],
[0, 1, 0],
[0, 1, 0],
[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 0, 1]])
These indicator columns are dummy variables where the values code for the group membership.
Now the \(\bvec\) vector will be:
When we estimate these using the least squares method, what estimates will we get for \(\bhat\)?
B = npl.pinv(X) @ psychopathy
B
array([10.74225, 11.3355 , 18.03425])
print('Berkeley mean:', np.mean(psychopathy[:4]))
print('Stanford mean:', np.mean(psychopathy[4:8]))
print('MIT mean:', np.mean(psychopathy[8:]))
Berkeley mean: 10.74225
Stanford mean: 11.3355
MIT mean: 18.03425
It looks like the MIT students are a bit more psychopathic. Are they more psychopathic than Berkeley and Stanford?
We can use a contrast to test whether the mean for the MIT students is greater than the mean of (mean for Berkeley, mean for Stanford):
B, t, df, p = t_stat(psychopathy, X, [-0.5, -0.5, 1])
t, p
(array([[2.340356]]), array([[0.021997]]))
Ah — yes — just as we suspected.
The model above expresses the effect of group membership. It is the expression of a one-way analysis of variance (ANOVA) model using \(\yvec = \Xmat \bvec + \evec\).
ANCOVA in the General Linear Model#
Our formulation \(\yvec = \Xmat \bvec + \evec\) makes it very easy to add extra regressors to models with group membership. For example, we can easily make a simple ANCOVA model (analysis of covariance).
ANCOVA is a specific term for the case where we have a model with both group membership (ANOVA model) and one or more continuous covariates.
For example, we can add back our clamminess score to the mix. Does it explain anything once we know which school the student is at?
X = np.column_stack((berkeley_indicator,
stanford_indicator,
mit_indicator,
clammy))
X
array([[1. , 0. , 0. , 0.389],
[1. , 0. , 0. , 0.2 ],
[1. , 0. , 0. , 0.241],
[1. , 0. , 0. , 0.463],
[0. , 1. , 0. , 4.585],
[0. , 1. , 0. , 1.097],
[0. , 1. , 0. , 1.642],
[0. , 1. , 0. , 4.972],
[0. , 0. , 1. , 7.957],
[0. , 0. , 1. , 5.585],
[0. , 0. , 1. , 5.527],
[0. , 0. , 1. , 6.964]])
We test the independent effect of the clamminess score with a contrast on the clammy slope parameter:
B, t, df, p = t_stat(psychopathy, X, [0, 0, 0, 1])
t, p
(array([[-0.010661]]), array([[0.504122]]))
It looks like there’s not much independent effect of clamminess. The MIT students seem to have clammy hands, and once we know that the student is from MIT, the clammy score is not as useful.
Displaying the design matrix as an image#
We can show the design as an image, by scaling the values with columns.
We scale within columns because we care more about seeing variation within the regressor than between regressors. For example, if we have a regressor varying between 0 and 1, and another between 0 and 1000, without scaling, the column with the larger numbers will swamp the variation in the column with the smaller numbers.
def scale_design_mtx(X):
"""utility to scale the design matrix for display
This scales the columns to their own range so we can see the variations
across the column for all the columns, regardless of the scaling of the
column.
"""
mi, ma = np.min(X, axis=0), np.max(X, axis=0)
# Vector that is True for columns where values are not
# all almost equal to each other
col_neq = (ma - mi) > 1.e-8
Xs = np.ones_like(X)
# Leave columns with same value throughout with 1s
# Scale other columns to min, max in column
mi = mi[col_neq]
ma = ma[col_neq]
Xs[:,col_neq] = (X[:,col_neq] - mi)/(ma - mi)
return Xs
Then we can display the scaled design with a title and some default image display parameters, to see our ANCOVA design at a glance.
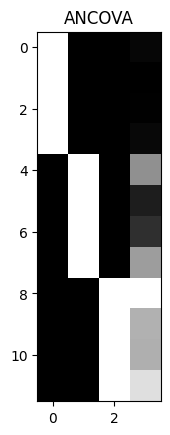
plt.imshow(scale_design_mtx(X), cmap='gray')
plt.title('ANCOVA')
Text(0.5, 1.0, 'ANCOVA')