Reshaping and three-dimensional arrays#
import numpy as np
Into the third dimension#
As we discussed in the three-dimensional arrays page page, one-dimensional and two-dimensional arrays are easy to think about. For example we can think of a 2D array as a table or a spreadsheet, with rows and columns.
A three-dimensional array takes a little bit more work to visualize, and get used to.
Reshaping a three-dimensional array#
You have already seen the algorithm for reshaping in one and two dimensions.
NumPy uses the same algorithm for reshaping a three-dimensional array.
We start with a one-dimensional array:
arr_1d = np.arange(24)
arr_1d.shape
(24,)
arr_1d
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23])
Then, reshape to three dimensions.
arr_3d = np.reshape(arr_1d, (2, 3, 4))
arr_3d
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
Remember from the three-dimensional arrays page page that we can
read the shape of arr_3d - (2, 3, 4) - as “two rows, three columns, four
planes”.
Let us translate that into the output of arr_3d as NumPy shows it. If we
picture arr_3d in physical space, it would be four planes stacked in a line,
each containing 2 rows and 3 columns.
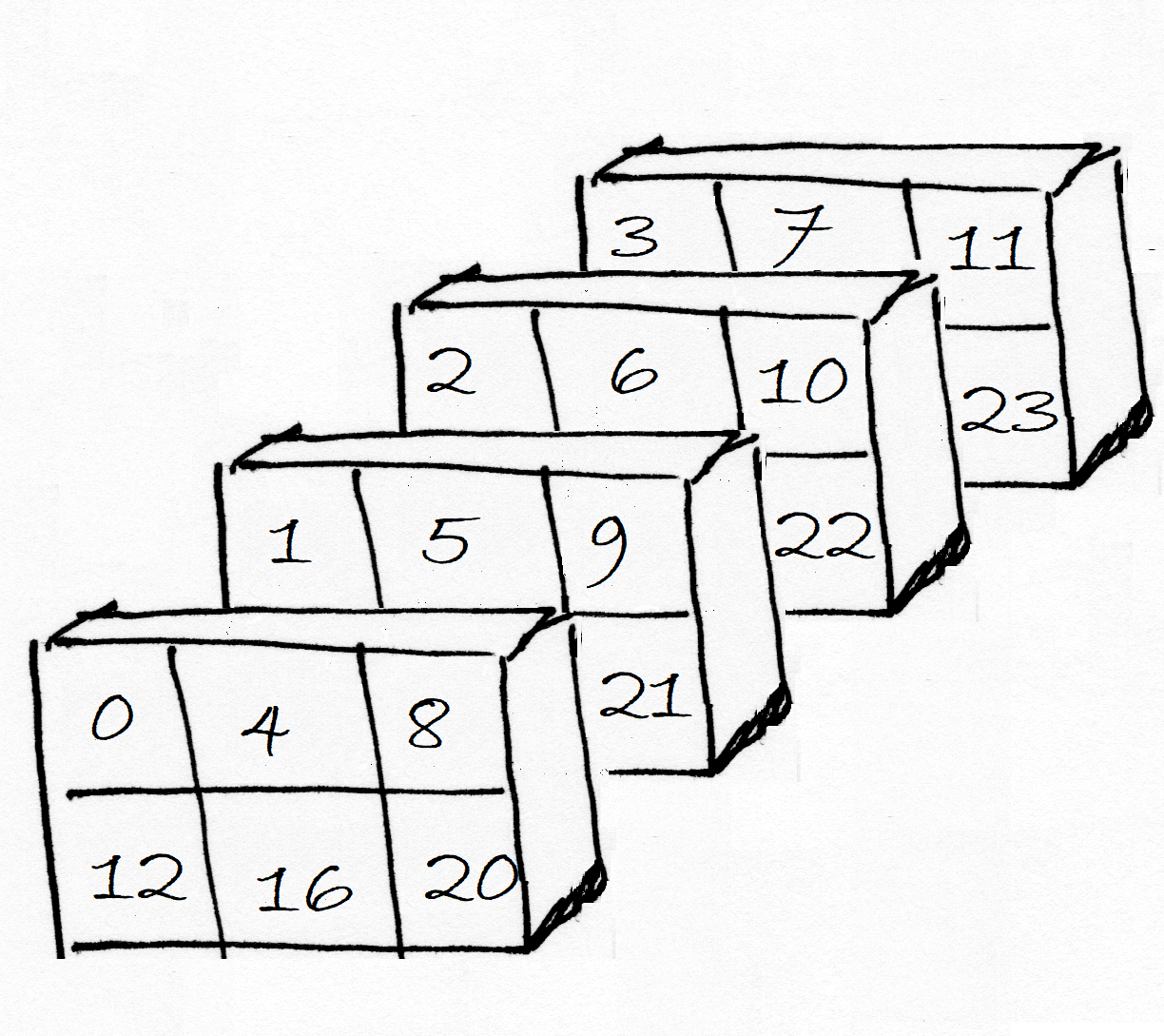
Notice too that Numpy has filled in the 3D array in the order:
plane, then
column, then
row.
That is, it fills in the last axis first, then the second to last, then the first axis.
This is the same way Numpy works for 2D arrays, when it fills in by:
column (last axis), then
row (first axis).
That means, as in the diagram above, that the first plane will get every 4th value from the original 1D array, because:
0, 1, 2, 3 fills the first row, first column, over the planes. We see 0 in the first row, first column of the first plane.
4, 5, 6, 7 fills the first row, second column, over the planes. We see 4 in the first row, second column, first plane. And so on.
For example, here, as in the diagram, is the first plane.
# The First plane.
arr_3d[:, :, 0]
array([[ 0, 4, 8],
[12, 16, 20]])
However, you will see above, and below, that NumPy is showing us the two slices over the first dimension, when we ask to see the array values:
# The default display shows the array by *rows*.
# Each row is 3 columns and 4 planes.
arr_3d
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
print('First row of data from 3D array:\n', arr_3d[0, :, :])
print('Second row of data from 3D array:\n', arr_3d[1, :, :])
First row of data from 3D array:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
Second row of data from 3D array:
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
To think about what array this is, imagine tipping the bottom of each 2D array towards you from the plane of the screen, and look at these tipped planes from the left, so the 0 sits nearly on top of 12, in the plane of the screen, and 4 sits nearly on top of 16, a little forward of the plane of the screen.
Compare the NumPy outputs to the image above, to make sure you can visualize the array from both perspectives.
We can reshape to one dimension in the same way as we did for the 2D arrays:
# Reshape to 1D array with 24 elements.
np.reshape(arr_3d, (24,))
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23])
# Reshape to 1D array, using all the elements (24 in this case).
np.reshape(arr_3d, (-1,))
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23])
# Reshape to 1D using dedicated Numpy function.
np.ravel(arr_3d)
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23])
To get the elements of the 1D array, NumPy first fetches values across the last axis (the depth or plane axis), then the second to last (column) axis, then the first (row) axis.
When reshaping to three dimensions, NumPy fills out the last, then second, then first dimensions (last to first):
arr_3d = np.reshape(arr_1d, (2, 3, 4))
arr_3d
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])




